In this lesson, the students will be able to:
Students will be able to:
Reference: NCERT Book Alignment
The lesson is aligned with the NCERT Grade 11 Physics Textbook, Chapter 7: Gravitation, Section 3 – The Universal Law Of Gravitation.
By the end of the lesson, students will be able to:
Universal Law of Gravitation introduces students to Newton’s idea that the same gravitational force responsible for the falling of objects on Earth also governs the motion of celestial bodies. The topic explains how Newton compared the moon’s centripetal acceleration with the acceleration due to gravity on Earth and inferred that gravitational influence decreases with distance.
This section then formally states the Universal Law of Gravitation, which describes that every mass in the universe attracts every other mass with a force proportional to the product of their masses and inversely proportional to the square of the distance between them. The mathematical and vector forms of the law are presented, along with key characteristics such as its attractive nature, central force behavior, and inverse-square dependence.
| Title | Approximate Duration | Procedure | Reference Material |
|---|---|---|---|
| Engage | 5 | Show two scenarios: an apple falling and the moon orbiting Earth. Pose question: “Is the force acting on the apple similar to the force keeping the moon in orbit?” Ask students to guess how gravitational force changes with distance. | Slides |
| Explore | 10 |
| Slides + Virtual Lab |
| Explain | 10 | Explain:
| Slides |
| Evaluate | 10 | Students will attempt the Self Evaluation task on LMS | Virtual Lab |
| Extend | 5 | Discussion:
| Slides |
Gravitation is a fundamental force of nature responsible for the attraction between any two masses in the universe. This topic introduces students to Newton’s Gravitational Law, which states that every object attracts every other object with a force that depends on their masses and the distance between them. This universal law not only explains everyday phenomena such as falling objects but also governs large-scale cosmic events like planetary motion, satellite orbits, and the structure of the universe. The topic builds the foundation for understanding how gravity shapes both terrestrial and celestial systems.
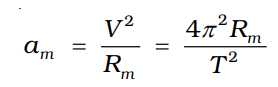
Centripetal Force and Planetary Motion
Kepler’s laws describe how planets move around the Sun. Newton showed that the gravitational force between the Sun and planets provides the necessary centripetal force required for circular and elliptical orbits. The decrease in gravitational influence with distance explains why objects orbit instead of falling directly into one another. The centripetal acceleration can be given as:
Universal Law of Gravitation
Newton’s Universal Law of Gravitation states that every particle of mass m1 in the universe attracts every other particle of mass m2 separated by a distance r with a force that is:
Mathematically,
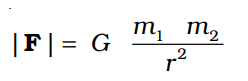
This force acts along the line joining the two masses and is always attractive. The Universal Law of Gravitation helps explain natural phenomena such as planetary orbits, the tides, the motion of satellites, and the formation of galaxies.
Vector Form Of Gravitational Force
The Gravitational Force of point mass m2 due to another point mass m1 can be expressed as a vector form as:
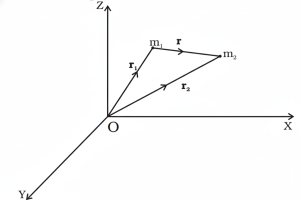
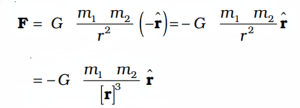
Where r is a position vector from m1 to m2 given as r = r2 – r1
Net Gravitational Force for Multiple Point Masses
The Gravitational Force on point mass m1 due to multiple point masses m2 ,m3, m4 can be expressed as a vector sum of all the forces acting on m1 and can be mathematically written as:
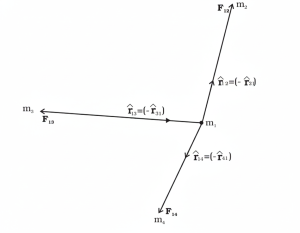
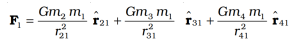
Gravitational Constant (G)
The constant of proportionality in Newton’s equation, represented by ( G ), is known as the universal gravitational constant. Henry Cavendish first measured its value using a torsion balance experiment. The magnitude of ( G ) determines the strength of the gravitational force between two masses.
Gravitational Field and Field Lines
A gravitational field is the region around a mass where it exerts a gravitational force on another mass. The gravitational field strength (( g )) at a point is the force experienced by a unit mass placed at that point. Gravitational field lines point toward the mass producing the field, showing that gravity is always attractive.
This is the list of vocabulary terms used throughout the lesson.
Welcome to the Gravitation Virtual Reality (VR) Lab!
In this exciting simulation, you will explore one of the most powerful forces in the universe — gravity.
Gravity is the invisible force that pulls objects toward each other. It is the reason why a ball falls back to the ground when you throw it upward and why the Earth moves around the Sun in a perfect orbit.
In this virtual lab, you will get to see gravity in action, experiment with how mass and distance affect gravitational force, and truly understand how this universal force shapes our world and the universe. Through guided scenes, students will deepen their understanding of the scalar and vector forms of gravitational force and learn how to compute net gravitational force due to multiple bodies.
Step 1: Revolution of Earth around Sun
Step 2: Scalar Form of Gravitational Law
Step 3: Vector Form of Gravitational Law
Step 4: Net Gravitational Force from Multiple Point Masses
Step 5: Simulation – Multiple-Body Gravitational System
Step 6: Evaluation