The Potential Energy of Spring

Content Standards

In this lesson, the students will be able to:

Understand that spring force is a conservative force and work done is path independent.
Derive and interpret the expression for work done by a spring force.
Explain how work done in stretching/compressing a spring leads to elastic potential energy.
Represent spring force and potential energy relationships using graphs.

Performance Standards

Students will be able to:

Correctly calculate the work done by a spring force for given displacements.
Evaluate spring potential energy in various scenarios.
Demonstrate understanding through numerical problems.
Interpret force–displacement and energy–displacement graphs for a spring.
Explain the conservation of mechanical energy in a spring–mass system.

Alignment Standards

Reference: NCERT Book Alignment

The lesson is aligned with the NCERT Grade 11 Physics Textbook, Chapter 5: Work Energy and Power, Section 9 – Potential Energy Of A Spring.

Learning Objectives

By the end of the lesson, students will be able to:

State and apply Hooke’s Law for an ideal spring.
Derive and explain the expression for work done by a spring force.
Describe why spring force is considered a conservative force.
Define and compute elastic potential energy stored in a spring.
Use the energy expression in solving real-life and numerical problems.

Prerequisites (Prior Knowledge)

Concept of work done by a constant and variable force.
Idea of potential energy for conservative forces (e.g., gravitational potential energy).
Basic understanding of graphs of force vs displacement.

Introduction

The study of potential energy of a spring forms a key part of the concept of energy in mechanics. A spring force is a variable, conservative force governed by Hooke’s Law, Fs=−kx. When a spring is stretched or compressed, mechanical work is done against the restoring force, and this work is stored as elastic potential energy. The relationship V(x)=kx2/2 emerges directly from calculating the work done in deforming an ideal spring, and it provides an essential foundation for understanding oscillatory motion, SHM, and energy conservation in mechanical systems.

Timeline (40 Minutes)

Title	Approximate Duration	Procedure	Reference Material
Engage	5	Show a short demonstration: stretching a common spring or rubber band. Ask: “Where does the energy go when we stretch a spring? Why does it bounce back?” Lead students to recognize that energy must be stored in some form.	Slides
Explore	10	Students explore the VR lab for potential energy.	Slides + Virtual Lab
Explain	10	Use textbook content to formally establish: Hooke’s Law, Fs=−kx Work done by spring force during extension: Work done by external force: Definition of potential energy of a spring Conservation of Potential Energy and Total Mechanical Energy of the system. Interpret the parabolic graph of potential energy vs displacement.	Slides
Evaluate	10	Students will attempt the Self Evaluation task on LMS.	Virtual Lab
Extend	5	Solve Textbook Example 5.8	Slides

The Potential Energy of Spring

Introduction

When a spring is stretched or compressed, work is done against the restoring force of the spring. This work is stored in the spring in the form of elastic potential energy. The study of spring potential energy helps us understand elastic forces, work done by variable forces, and the energy transformations involved in mechanical systems. This concept is also important for later chapters such as Oscillations and Mechanical Energy Conservation.

Theory

Hooke’s Law
Springs follow Hooke’s Law within the elastic limit. According to this law, the restoring force developed in a spring is proportional to its displacement from the equilibrium position:

Fs = -kx

k is the spring constant, a measure of the stiffness of the spring.
x is the displacement from the natural length of the spring.
The negative sign indicates that the restoring force acts opposite to the direction of displacement.
The unit of the k is N/m.

Work Done By a Spring Force

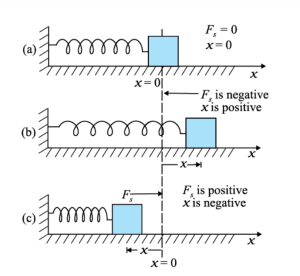
To stretch the block of mass m attached to a spring with displacement xm, the work done by the spring force is given as:

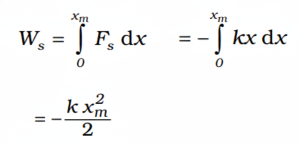
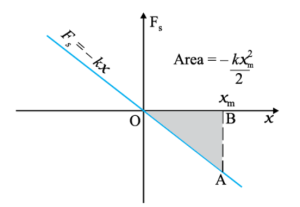
This expression can be also obtained by finding the area of the shaded region for the Force vs displacement graph.

The work done by the external force is positive since it overcomes spring force and can be written as:

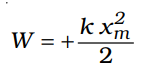
Similarly, for compression of the spring with displacement xc the work done by the spring force is given as,

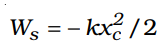
And work done by external force for compression is also positive and given as:

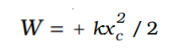
The above case was to discuss the work done by the spring force when the block is displaced from equilibrium position as shown in the diagram above.
If the block is moved from the initial displacement xi to a final displacement xf , then work done by a spring force is

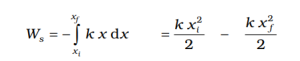
Thus, the work done by the spring force depends only on the end points. Specifically, if the block is pulled from xi and allowed to return to xi then the work done is zero for a cyclic process.

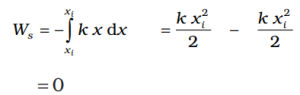
We have explicitly demonstrated that the spring force (i) is position dependent only as first stated by Hooke, (Fs = − kx); (ii) does work which only depends on the initial and final positions). Thus, the spring force is a conservative force.

Potential Energy of a Spring

We define the potential energy V(x) of the spring to be zero when the block and spring system is in the equilibrium position. For an extension (or compression) x the above analysis suggests that

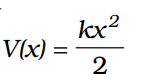
This expression shows that the potential energy depends on the square of displacement. Thus, doubling the extension results in four times the energy.

Characteristics of Spring Potential Energy

The function V(x) is minimum (zero) at the equilibrium position.
Since the spring force is conservative, the work done depends only on the initial and final positions.
The potential energy curve for a spring is a parabola when plotted against displacement.

Total Mechanical Energy

If the block of mass m is extended to xm and released from rest, then its total mechanical energy at any arbitrary point x, where x lies between – xm and + xm, will be given by

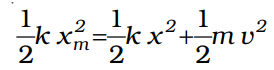
The total mechanical energy is conserved, suggesting that the speed and the kinetic energy will be maximum at the equilibrium position, x=0

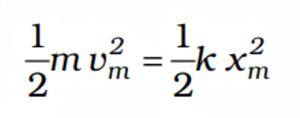
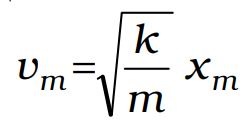
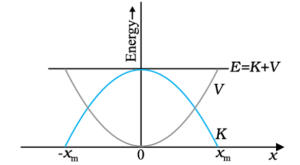
Graphical Representation of Total Mechanical Energy

Parabolic plots of the potential energy V and kinetic energy K of a block attached to a spring obeying Hooke’s law. The two plots are complementary, one decreasing as the other increases. The total mechanical energy E = K + V remains constant.

Vocabulary

This is the list of vocabulary terms used throughout the lesson.

Hooke’s Law – Law stating that restoring force is directly proportional to displacement.
Spring Constant (k) – A measure of how stiff or flexible a spring is.
Elastic Limit – Maximum stretch or compression for which Hooke’s law is valid.
Restoring Force – The force that pulls the spring back toward equilibrium.
Displacement (x) – Distance from the natural length of the spring.
Elastic Potential Energy – Energy stored in a spring when deformed.
Conservative Force – A force for which work done is independent of the path taken.
Equilibrium Position – The natural, unstressed length of the spring.
Variable Force – A force whose magnitude changes with displacement.
Force–Displacement Graph – A graph showing how restoring force varies with extension or compression.

The Potential Energy of Spring

Introduction

Welcome to the Virtual Reality (VR) Lab on Potential Energy of a Spring. This VR experience will help you observe how a spring behaves when stretched or compressed and understand how elastic potential energy is stored. You will interact with springs, forces, and energy graphs in a 3D immersive environment. This guide will help you navigate each part of the VR lab smoothly.

Key Features

Interactive Spring Model
3D- Immersive Environment
Self Evaluation

Step-by-Step Procedure for VR Experience

Step 1: Introduction

Introduction to Spring Mechanics.

Step 2: Restoring Force and Displacement

Look around to identify the spring system and measurement scale.
You will see the initial equilibrium state of the spring.

Step 3: Graphical Representation Of Force and Energy

Identify how the linear nature of the graph matches Hooke’s Law
Observe how energy grows faster when the displacement increases.

Step 4: Evaluation

After interaction, students proceed to the quiz:
- 2 MCQs